In Section 3.3 we learned about extreme values -- the largest and smallest values a function attains on an interval. We motivated our interest in such values by discussing how it made sense to want to know the highest/lowest values of a stock or the fastest/slowest an object was moving. In this section, we apply the concepts of extreme values to solve 'word problems,' i.e., problems stated in terms of situations that require us to create the appropriate mathematical framework in which to solve the problem.
We start with a classic example which is followed by a discussion of the topic of optimization.
Section 4-8: Optimization. Find two positive numbers whose sum is 300 and whose product is a maximum. Solution; Find two positive numbers whose product is 750 and for which the sum of one and 10 times the other is a minimum. So it looks like my volume at 3.89 is approximately equal to 1,056 cubic inches. Or you could say that we hit a maximum when x is approximately equal to 3.89. So far, we've just set up our maximization problem, and we've looked at it graphically. In the next video, we'll try to solve it analytically using some of our calculus tools. Maximize Power Delivered to Circuits Optimization Problem. The first derivative is used to maximize (optimize) the power delivered to a load in electronic circuits. Optimization of One Variable For what value(s) of x will the function f (x) = x 3-2x 2 - 5x be largest on the interval - 10, 10? This problem is asking us to find the absolute maximum on the interval. One way to do this is to graph the function and determine by inspection what the absolute maximum is. However, this is a very time-consuming.
Solving Optimization Problems over a Closed, Bounded Interval
Example (PageIndex{1}): Optimization: perimeter and area
A man has 100 feet of fencing, a large yard, and a small dog. He wants to create a rectangular enclosure for his dog with the fencing that provides the maximal area. What dimensions provide the maximal area?
Solution
One can likely guess the correct answer -- that is great. We will proceed to show how calculus can provide this answer in a context that proves this answer is correct.
It helps to make a sketch of the situation. Our enclosure is sketched twice in Figure (PageIndex{1}), either with green grass and nice fence boards or as a simple rectangle. Either way, drawing a rectangle forces us to realize that we need to know the dimensions of this rectangle so we can create an area function -- after all, we are trying to maximize the area.
We let (x) and (y) denote the lengths of the sides of the rectangle. Clearly,
[text{Area}=xy.]
We do not yet know how to handle functions with 2 variables; we need to reduce this down to a single variable. We know more about the situation: the man has 100 feet of fencing. By knowing the perimeter of the rectangle must be 100, we can create another equation:
[text{Perimeter} = 100 = 2x+2y.]
We now have 2 equations and 2 unknowns. In the latter equation, we solve for (y):
[y = 50-x.]
Now substitute this expression for (y) in the area equation:
[ text{Area} = A(x) = x(50-x).]
Note we now have an equation of one variable; we can truly call the Area a function of (x).
This function only makes sense when (0leq x leq 50), otherwise we get negative values of area. So we find the extreme values of (A(x)) on the interval ([0,50]).
To find the critical points, we take the derivative of (A(x)) and set it equal to 0, then solve for (x).
5.6 Optimization Problemsap Calculus 2nd Edition

[begin{align} A(x) &= x(50-x) &= 50x-x^2 A'(x) &= 50-2x end{align}]
We solve (50-2x=0) to find (x=25); this is the only critical point. We evaluate (A(x)) at the endpoints of our interval and at this critical point to find the extreme values; in this case, all we care about is the maximum.
Clearly (A(0)=0) and (A(50)=0), whereas (A(25) = 625 text{ft}^2). This is the maximum. Since we earlier found (y = 50-x), we find that (y) is also (25). Thus the dimensions of the rectangular enclosure with perimeter of 100 ft. with maximum area is a square, with sides of length 25 ft.
This example is very simplistic and a bit contrived. (After all, most people create a design then buy fencing to meet their needs, and not buy fencing and plan later.) But it models well the necessary process: create equations that describe a situation, reduce an equation to a single variable, then find the needed extreme value.
'In real life,' problems are much more complex. The equations are often not reducible to a single variable (hence multi--variable calculus is needed) and the equations themselves may be difficult to form. Understanding the principles here will provide a good foundation for the mathematics you will likely encounter later.
We outline here the basic process of solving these optimization problems.
Key Idea 6: Solving Optimization Problems
- Understand the problem. Clearly identify what quantity is to be maximized or minimized. Make a sketch if helpful.
- Create equations relevant to the context of the problem, using the information given. (One of these should describe the quantity to be optimized. We'll call this the fundamental equation.)
- If the fundamental equation defines the quantity to be optimized as a function of more than one variable, reduce it to a single variable function using substitutions derived from the other equations.
- Identify the domain of this function, keeping in mind the context of the problem.
- Find the extreme values of this function on the determined domain.
- Identify the values of all relevant quantities of the problem.
We will use Key Idea 6 in a variety of examples.
Example (PageIndex{2}): Optimization: perimeter and area
Here is another classic calculus problem: A woman has a 100 feet of fencing, a small dog, and a large yard that contains a stream (that is mostly straight). She wants to create a rectangular enclosure with maximal area that uses the stream as one side. (Apparently, her dog won't swim away.) What dimensions provide the maximal area?
Solution
We will follow the steps outlined by Key Idea 6.
- We are maximizing area. A sketch of the region will help; Figure (PageIndex{2}) gives two sketches of the proposed enclosed area. A key feature of the sketches is to acknowledge that one side is not fenced.
- We want to maximize the area; as in the example before, [text{Area} = xy.[ This is our fundamental equation. This defines area as a function of two variables, so we need another equation to reduce it to one variable.
We again appeal to the perimeter; here the perimeter is [text{Perimeter} = 100 = x+2y.[ Note how this is different than in our previous example. - We now reduce the fundamental equation to a single variable. In the perimeter equation, solve for (y): (y = 50 - x/2). We can now write Area as [text{Area} = A(x) = x(50-x/2) = 50x - frac12x^2.[ Area is now defined as a function of one variable.
- We want the area to be nonnegative. Since (A(x) = x(50-x/2)), we want (xgeq 0) and (50-x/2geq 0). The latter inequality implies that (xleq100), so (0leq xleq 100).
- We now find the extreme values. At the endpoints, the minimum is found, giving an area of 0.
Find the critical points. We have (A'(x) = 50-x); setting this equal to 0 and solving for (x) returns (x=50). This gives an area of [A(50) = 50(25) = 1250.[
| (x) | (A(x)) |
| 0 | 0 |
| 50 | (50)(25) |
| 100 | 0 |
- We earlier set (y = 50-x/2); thus (y = 25). Thus our rectangle will have two sides of length 25 and one side of length 50, with a total area of 1250 ft(^2).
Keep in mind as we do these problems that we are practicing a process; that is, we are learning to turn a situation into a system of equations. These equations allow us to write a certain quantity as a function of one variable, which we then optimize.
Example (PageIndex{3}): Optimization: minimizing cost
A power line needs to be run from a power station located on the beach to an offshore facility. Figure (PageIndex{3}) shows the distances between the power station to the facility.
It costs $50/ft. to run a power line along the land, and $130/ft. to run a power line under water. How much of the power line should be run along the land to minimize the overall cost? What is the minimal cost?
Solution
We will follow the strategy of Key Idea 6 implicitly, without specifically numbering steps.
There are two immediate solutions that we could consider, each of which we will reject through 'common sense.' First, we could minimize the distance by directly connecting the two locations with a straight line. However, this requires that all the wire be laid underwater, the most costly option. Second, we could minimize the underwater length by running a wire all 5000 ft. along the beach, directly across from the offshore facility. This has the undesired effect of having the longest distance of all, probably ensuring a non--minimal cost.
The optimal solution likely has the line being run along the ground for a while, then underwater, as the figure implies. We need to label our unknown distances -- the distance run along the ground and the distance run underwater. Recognizing that the underwater distance can be measured as the hypotenuse of a right triangle, we choose to label the distances as shown in Figure (PageIndex{4}).
By choosing (x) as we did, we make the expression under the square root simple. We now create the cost function.
[
begin{array}{ccccc}
text{Cost} &=& text{land cost} &+ & text{water cost}
& & text{$50}times text{land distance} &+& text{$130}times text{water distance}
& & 50(5000-x) &+& 130sqrt{x^2+1000^2}.
end{array}
]
So we have (c(x) = 50(5000-x)+ 130sqrt{x^2+1000^2}). This function only makes sense on the interval ([0,5000]). While we are fairly certain the endpoints will not give a minimal cost, we still evaluate (c(x)) at each to verify.
[c(0) = 380,000 quadquad c(5000) approx 662,873.]
We now find the critical values of (c(x)). We compute (c'(x)) as
[c'(x) = -50+frac{130x}{sqrt{x^2+1000^2}}.]
Recognize that this is never undefined. Setting (c'(x)=0) and solving for (x), we have:
[ begin{align} -50+frac{130x}{sqrt{x^2+1000^2}} &= 0 frac{130x}{sqrt{x^2+1000^2}} &= 50 frac{130^2x^2}{x^2+1000^2} &= 50^2 130^2x^2 &= 50^2(x^2+1000^2) 130^2x^2-50^2x^2 &= 50^2cdot1000^2 (130^2-50^2)x^2 &= 50,000^2 x^2 &= frac{50,000^2}{130^2-50^2} x &= frac{50,000}{sqrt{130^2-50^2}} x & = frac{50,000}{120} =416frac23approx 416.67. end{align}]
Evaluating (c(x)) at (x=416.67) gives a cost of about $370,000. The distance the power line is laid along land is (5000-416.67 = 4583.33) ft., and the underwater distance is (sqrt{416.67^2+1000^2} approx 1083) ft.
Example (PageIndex{4}): Maximizing the Volume of a Box
An open-top box is to be made from a (24) in. by (36) in. the piece of cardboard by removing a square from each corner of the box and folding up the flaps on each side. What size square should be cut out of each corner to get a box with the maximum volume?
Solution
Step 1: Let (x) be the side length of the square to be removed from each corner (Figure (PageIndex{3})). Then, the remaining four flaps can be folded up to form an open-top box. Let (V) be the volume of the resulting box.
Step 2: We are trying to maximize the volume of a box. Therefore, the problem is to maximize (V).
Step 3: As mentioned in step (2), are trying to maximize the volume of a box. The volume of a box is
[V=L⋅W⋅H nonumber,]
where (L,W,)and (H) are the length, width, and height, respectively.
Step 4: From Figure (PageIndex{3}), we see that the height of the box is (x) inches, the length is (36−2x) inches, and the width is (24−2x) inches. Therefore, the volume of the box is
[ begin{align*} V(x) &=(36−2x)(24−2x)x [5pt] &=4x^3−120x^2+864x end{align*}.]
Step 5: To determine the domain of consideration, let’s examine Figure (PageIndex{3}). Certainly, we need (x>0.) Furthermore, the side length of the square cannot be greater than or equal to half the length of the shorter side, (24) in.; otherwise, one of the flaps would be completely cut off. Therefore, we are trying to determine whether there is a maximum volume of the box for (x) over the open interval ((0,12).) Since (V) is a continuous function over the closed interval ([0,12]), we know (V) will have an absolute maximum over the closed interval. Therefore, we consider (V) over the closed interval ([0,12]) and check whether the absolute maximum occurs at an interior point.
Step 6: Since (V(x)) is a continuous function over the closed, bounded interval ([0,12], V) must have an absolute maximum (and an absolute minimum). Since (V(x)=0) at the endpoints and (V(x)>0) for (0<x<12,) the maximum must occur at a critical point. The derivative is
(V′(x)=12x^2−240x+864.)
To find the critical points, we need to solve the equation
(12x^2−240x+864=0.)
Dividing both sides of this equation by (12), the problem simplifies to solving the equation
(x^2−20x+72=0.)
Using the quadratic formula, we find that the critical points are
[begin{align*} x&=dfrac{20±sqrt{(−20)^2−4(1)(72)}}{2} [5pt] &=dfrac{20±sqrt{112}}{2} [5pt] &=dfrac{20±4sqrt{7}}{2} [5pt] &=10±2sqrt{7} end{align*}.]

Since (10+2sqrt{7}) is not in the domain of consideration, the only critical point we need to consider is (10−2sqrt{7}). Therefore, the volume is maximized if we let (x=10−2sqrt{7}, in.) The maximum volume is
[V(10−2sqrt{7})=640+448sqrt{7}≈1825,in.^3 nonumber ]
as shown in the following graph.
Watch a video about optimizing the volume of a box.
Exercise (PageIndex{2})
Suppose the dimensions of the cardboard in Example (PageIndex{2}) are 20 in. by 30 in. Let (x) be the side length of each square and write the volume of the open-top box as a function of (x). Determine the domain of consideration for (x).
The volume of the box is (L⋅W⋅H.)
(V(x)=x(20−2x)(30−2x).) The domain is ([0,10]).
Example (PageIndex{5}): Minimizing Travel Time
An island is (2,mi) due north of its closest point along a straight shoreline. A visitor is staying at a cabin on the shore that is (6,mi) west of that point. The visitor is planning to go from the cabin to the island. Suppose the visitor runs at a rate of (8,mph) and swims at a rate of (3,mph). How far should the visitor run before swimming to minimize the time it takes to reach the island?
Solution
Step 1: Let (x) be the distance running and let (y) be the distance swimming (Figure (PageIndex{5})). Let (T) be the time it takes to get from the cabin to the island.
Step 2: The problem is to minimize (T).
Step 3: To find the time spent traveling from the cabin to the island, add the time spent running and the time spent swimming. Since Distance = Rate × Time ((D=R×T),) the time spent running is
(T_{running}=dfrac{D_{running}}{R_{running}}=dfrac{x}{8}),
and the time spent swimming is
(T_{swimming}=dfrac{D_{swimming}}{R_{swimming}}=dfrac{y}{3}).
Therefore, the total time spent traveling is
(T=dfrac{x}{8}+dfrac{y}{3}).
Step 4: From Figure (PageIndex{5}), the line segment of (y) miles forms the hypotenuse of a right triangle with legs of length (2mi) and (6−xmi). Therefore, by the Pythagorean theorem, (2^2+(6−x)^2=y^2), and we obtain (y=sqrt{(6−x)^2+4}). Thus, the total time spent traveling is given by the function
(T(x)=dfrac{x}{8}+dfrac{sqrt{(6−x)^2+4}}{3}).
Step 5: From Figure (PageIndex{5}), we see that (0≤x≤6). Therefore, ([0,6]) is the domain of consideration.
Step 6: Since (T(x)) is a continuous function over a closed, bounded interval, it has a maximum and a minimum. Let’s begin by looking for any critical points of (T) over the interval ([0,6].) The derivative is
[begin{align*} T′(x) &=dfrac{1}{8}−dfrac{1}{2}dfrac{[(6−x)^2+4]^{−1/2}}{3}⋅2(6−x) [5pt] &=dfrac{1}{8}−dfrac{(6−x)}{3sqrt{(6−x)^2+4}} end{align*}]
If (T′(x)=0,), then
[dfrac{1}{8}=dfrac{6−x}{3sqrt{(6−x)^2+4}} nonumber]
Therefore,
[3sqrt{(6−x)^2+4}=8(6−x). nonumber]
Squaring both sides of this equation, we see that if (x) satisfies this equation, then (x) must satisfy
[9[(6−x)^2+4]=64(6−x)^2,nonumber ]
which implies
[55(6−x)^2=36. nonumber]
We conclude that if (x) is a critical point, then (x) satisfies
[(x−6)^2=dfrac{36}{55}. nonumber]
Therefore, the possibilities for critical points are
[(x=6±dfrac{6}{sqrt{55}}.nonumber]
Since (x=6+6/sqrt{55}) is not in the domain, it is not a possibility for a critical point. On the other hand, (x=6−6/sqrt{55}) is in the domain. Since we squared both sides of Equation to arrive at the possible critical points, it remains to verify that (x=6−6/sqrt{55}) satisfies Equation. Since (x=6−6/sqrt{55}) does satisfy that equation, we conclude that (x=6−6/sqrt{55}) is a critical point, and it is the only one. To justify that the time is minimized for this value of x, we just need to check the values of (T(x)) at the endpoints (x=0) and (x=6), and compare them with the value of (T(x)) at the critical point (x=6−6/sqrt{55}). We find that (T(0)≈2.108h) and (T(6)≈1.417h), whereas
[T(6−6/sqrt{55})≈1.368h. nonumber]
Therefore, we conclude that (T) has a local minimum at (x≈5.19 mi).
Exercise (PageIndex{3})
Suppose the island is (1, mi) from shore, and the distance from the cabin to the point on the shore closest to the island is (15,mi). Suppose a visitor swims at the rate of (2.5,mph) and runs at a rate of (6,mph). Let (x) denote the distance the visitor will run before swimming, and find a function for the time it takes the visitor to get from the cabin to the island.
The time (T=T_{running}+T_{swimming}.)
[T(x)=dfrac{x}{6}+dfrac{sqrt{(15−x)^2+1}}{2.5} nonumber ]
In business, companies are interested in maximizing revenue. In the following example, we consider a scenario in which a company has collected data on how many cars it is able to lease, depending on the price it charges its customers to rent a car. Let’s use these data to determine the price the company should charge to maximize the amount of money it brings in.
Example (PageIndex{6}): Maximizing Revenue
Owners of a car rental company have determined that if they charge customers (p) dollars per day to rent a car, where (50≤p≤200), the number of cars (n) they rent per day can be modeled by the linear function (n(p)=1000−5p). If they charge ($50) per day or less, they will rent all their cars. If they charge ($200) per day or more, they will not rent any cars. Assuming the owners plan to charge customers between ($50) per day and ($200) per day to rent a car, how much should they charge to maximize their revenue?
Solution
Step 1: Let (p) be the price charged per car per day and let n be the number of cars rented per day. Let (R) be the revenue per day.

Step 2: The problem is to maximize (R.)
Step 3: The revenue (per day) is equal to the number of cars rented per day times the price charged per car per day—that is, (R=n×p.)
Step 4: Since the number of cars rented per day is modeled by the linear function (n(p)=1000−5p,) the revenue (R) can be represented by the function
[ begin{align*} R(p) &=n×p [5pt] &=(1000−5p)p [5pt] &=−5p^2+1000p.end{align*}]
Step 5: Since the owners plan to charge between ($50) per car per day and ($200) per car per day, the problem is to find the maximum revenue (R(p)) for (p) in the closed interval ([50,200]).
Step 6: Since (R) is a continuous function over the closed, bounded interval ([50,200]), it has an absolute maximum (and an absolute minimum) in that interval. To find the maximum value, look for critical points. The derivative is (R′(p)=−10p+1000.) Therefore, the critical point is (p=100) When (p=100, R(100)=$50,000.) When (p=50, R(p)=$37,500). When (p=200, R(p)=$0).
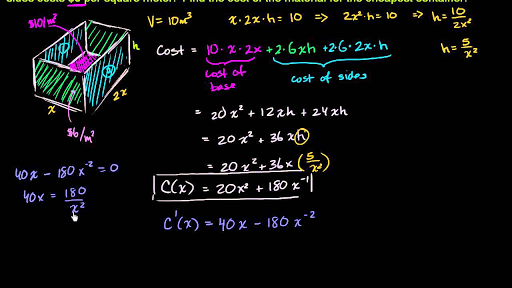
Therefore, the absolute maximum occurs at (p=$100). The car rental company should charge ($100) per day per car to maximize revenue as shown in the following figure.
Exercise (PageIndex{4})
A car rental company charges its customers (p) dollars per day, where (60≤p≤150). It has found that the number of cars rented per day can be modeled by the linear function (n(p)=750−5p.) How much should the company charge each customer to maximize revenue?
(R(p)=n×p,) where (n) is the number of cars rented and (p) is the price charged per car.
The company should charge ($75) per car per day.
Example (PageIndex{7}): Maximizing the Area of an Inscribed Rectangle
A rectangle is to be inscribed in the ellipse
[dfrac{x^2}{4}+y^2=1. nonumber ]
What should the dimensions of the rectangle be to maximize its area? What is the maximum area?
Solution
Step 1: For a rectangle to be inscribed in the ellipse, the sides of the rectangle must be parallel to the axes. Let (L) be the length of the rectangle and (W) be its width. Let (A) be the area of the rectangle.
Step 2: The problem is to maximize (A).
Step 3: The area of the rectangle is (A=LW.)
Step 4: Let ((x,y)) be the corner of the rectangle that lies in the first quadrant, as shown in Figure (PageIndex{7}). We can write length (L=2x) and width (W=2y). Since (dfrac{x^2}{4+y^2=1}) and (y>0), we have (y=sqrt{dfrac{1−x^2}{4}}). Therefore, the area is
(A=LW=(2x)(2y)=4xsqrt{dfrac{1−x^2}{4}}=2xsqrt{4−x^2})
Step 5: From Figure (PageIndex{7}), we see that to inscribe a rectangle in the ellipse, the (x)-coordinate of the corner in the first quadrant must satisfy (0<x<2). Therefore, the problem reduces to looking for the maximum value of (A(x)) over the open interval ((0,2)). Since (A(x)) will have an absolute maximum (and absolute minimum) over the closed interval ([0,2]), we consider (A(x)=2xsqrt{4−x^2}) over the interval ([0,2]). If the absolute maximum occurs at an interior point, then we have found an absolute maximum in the open interval.
Step 6: As mentioned earlier, (A(x)) is a continuous function over the closed, bounded interval ([0,2]). Therefore, it has an absolute maximum (and absolute minimum). At the endpoints (x=0) and (x=2, A(x)=0.) For (0<x<2, A(x)>0).
Therefore, the maximum must occur at a critical point. Taking the derivative of (A(x)), we obtain
[ begin{align*} A'(x) &=2sqrt{4−x^2}+2x⋅dfrac{1}{2sqrt{4−x^2}}(−2x) [5pt] &=2sqrt{4−x^2}−dfrac{2x^2}{sqrt{4−x^2}} [5pt] &=dfrac{8−4x^2}{sqrt{4−x^2}} . end{align*}]
To find critical points, we need to find where (A'(x)=0.) We can see that if (x) is a solution of
(dfrac{8−4x^2}{sqrt{4−x^2}}=0),
then (x) must satisfy
[8−4x^2=0. label{eq5a}]
Therefore, (x^2=2.) Thus, (x=±sqrt{2}) are the possible solutions of Equation. Since we are considering (x) over the interval ([0,2]), (x=sqrt{2}) is a possibility for a critical point, but (x=−sqrt{2}) is not. Therefore, we check whether (sqrt{2}) is a solution of Equation. Since (x=sqrt{2}) is a solution of Equation ref{eq5a}, we conclude that (sqrt{2}) is the only critical point of (A(x)) in the interval ([0,2]).
Therefore, (A(x)) must have an absolute maximum at the critical point (x=sqrt{2}). To determine the dimensions of the rectangle, we need to find the length (L) and the width (W). If (x=sqrt{2}) then
[y=sqrt{1−dfrac{(sqrt{2})^2}{4}}=sqrt{1−dfrac{1}{2}}=dfrac{1}{sqrt{2}}.]
Therefore, the dimensions of the rectangle are (L=2x=2sqrt{2}) and (W=2y=dfrac{2}{sqrt{2}}=sqrt{2}). The area of this rectangle is( A=LW=(2sqrt{2})(sqrt{2})=4.)
Exercise (PageIndex{5})
Modify the area function (A) if the rectangle is to be inscribed in the unit circle (x^2+y2^=1). What is the domain of consideration?
If ((x,y)) is the vertex of the square that lies in the first quadrant, then the area of the square is (A=(2x)(2y)=4xy.)
(A(x)=4xsqrt{1−x^2}.) The domain of consideration is ([0,1]).
Solving Optimization Problems when the Interval Is Not Closed or Is Unbounded
In the previous examples, we considered functions on closed, bounded domains. Consequently, by the extreme value theorem, we were guaranteed that the functions had absolute extrema. Let’s now consider functions for which the domain is neither closed nor bounded.
Many functions still have at least one absolute extrema, even if the domain is not closed or the domain is unbounded. For example, the function (f(x)=x^2+4) over ((−∞,∞)) has an absolute minimum of (4) at (x=0). Therefore, we can still consider functions over unbounded domains or open intervals and determine whether they have any absolute extrema. In the next example, we try to minimize a function over an unbounded domain. We will see that, although the domain of consideration is ((0,∞),) the function has an absolute minimum.
In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area. Consequently, we consider the modified problem of determining which open-topped box with a specified volume has the smallest surface area.
Example (PageIndex{8}): Minimizing Surface Area
A rectangular box with a square base, an open top, and a volume of (216 in.^3) is to be constructed. What should the dimensions of the box be to minimize the surface area of the box? What is the minimum surface area?
Solution
Step 1: Draw a rectangular box and introduce the variable (x) to represent the length of each side of the square base; let (y) represent the height of the box. Let (S) denote the surface area of the open-top box.
Step 2: We need to minimize the surface area. Therefore, we need to minimize (S).
Step 3: Since the box has an open top, we need only determine the area of the four vertical sides and the base. The area of each of the four vertical sides is (x⋅y.) The area of the base is (x^2). Therefore, the surface area of the box is
(S=4xy+x^2).
Step 4: Since the volume of this box is (x^2y) and the volume is given as (216in.^3), the constraint equation is
(x^2y=216).
Solving the constraint equation for (y), we have (y=dfrac{216}{x^2}). Therefore, we can write the surface area as a function of (x) only:
[S(x)=4x(dfrac{216}{x^2})+x^2.]
Therefore, (S(x)=dfrac{864}{x}+x^2).
Step 5: Since we are requiring that (x^2y=216), we cannot have (x=0). Therefore, we need (x>0). On the other hand, (x) is allowed to have any positive value. Note that as (x) becomes large, the height of the box (y) becomes correspondingly small so that (x^2y=216). Similarly, as (x) becomes small, the height of the box becomes correspondingly large. We conclude that the domain is the open, unbounded interval ((0,∞)). Note that, unlike the previous examples, we cannot reduce our problem to looking for an absolute maximum or absolute minimum over a closed, bounded interval. However, in the next step, we discover why this function must have an absolute minimum over the interval ((0,∞).)
Step 6: Note that as (x→0+^,S(x)→∞.) Also, as (x→∞, S(x)→∞). Since (S) is a continuous function that approaches infinity at the ends, it must have an absolute minimum at some (x∈(0,∞)). This minimum must occur at a critical point of (S). The derivative is
[S′(x)=−dfrac{864}{x^2}+2x.]
Therefore, (S′(x)=0) when (2x=dfrac{864}{x^2}). Solving this equation for (x), we obtain (x^3=432), so (x=sqrt[3]{432}=6sqrt[3]{2}.) Since this is the only critical point of (S), the absolute minimum must occur at (x=6sqrt[3]{2}) (see Figure (PageIndex{9})).
When (x=6sqrt[3]{2}), (y=dfrac{216}{(6sqrt[3]{2})^2}=3sqrt[3]{2}in). Therefore, the dimensions of the box should be (x=6sqrt[3]{2}in.) and (y=3sqrt[3]{2}in.) With these dimensions, the surface area is
[S(6sqrt[3]{2})=dfrac{864}{6sqrt[3]{2}}+(6sqrt[3]{2})^2=108sqrt[3]{4}in.^2]
Exercise (PageIndex{8})
Consider the same open-top box, which is to have volume (216in.^3). Suppose the cost of the material for the base is (20¢/in.^2) and the cost of the material for the sides is (30¢/in.^2) and we are trying to minimize the cost of this box. Write the cost as a function of the side lengths of the base. (Let (x) be the side length of the base and (y) be the height of the box.)
If the cost of one of the sides is (30¢/in.^2,) the cost of that side is (0.30xy.)
(c(x)=dfrac{259.2}{x}+0.2x^2) dollars
Example (PageIndex{9}): Minimizing Cost
An open-topped cylindrical can is to have volume (300, cm^3). The material for the bottom of the can costs (10, cents/cm^2), for its curved side costs (5 , cents/cm^2.) Find the dimensions of the can that minimize the cost of the can.
Solution
Step 1: Draw a cylindrical can and introduce the variable (r) to represent the radius of the circular base; let (h) represent the height of the can. Let (C) denote the cost to produce a can.
Step 2: Given: Volume of the can (V= 300). We need to minimize the cost. Therefore, we need to minimize (C).
Step 3: Since the can has an open top, we need only determine the cost to produce the bottom and the cost to produce the side.
The surface area of the curved side is (2 pi rh) The area of the bottom is (pi r^2). Therefore, the cost to produce the can is
(C=(5) 2 pi rh+ (10)pi r^2), with (r geq 0).

Step 4: Since the volume of this can ( pi r^2 h) and the volume is given as (300 ), the constraint equation is
(pi r^2 h=300).
Solving the constraint equation for (h), we have (h=dfrac{300}{pi r^2}). Therefore, we can write the cost as a function of (r) only:
(C=(5) 2 pi rdfrac{300}{pi r^2}+ (10)pi r^2).
Therefore, (C=dfrac{3000 }{ r}+ (10)pi r^2).
Step 5: Since we are requiring that (pi r^2 h=300), we cannot have (r=0). Therefore, we need (r>0). On the other hand, (r) is allowed to have any positive value. Note that as (r) becomes large, the height of the can (h) becomes correspondingly small so that (pi r^2 h=300). Similarly, as (r) becomes small, the height of the can becomes correspondingly large. We conclude that the domain is the open, unbounded interval ((0,∞)). In the next step, we discover why this function must have an absolute minimum over the interval ((0,∞).)
Step 6: Note that as (x→0+^, C(r)→∞.) Also, as (r→∞, C(r)→∞). Since (C) is a continuous function that approaches infinity at the ends, it must have an absolute minimum at some (r∈(0,∞)). This minimum must occur at a critical point of (C). The derivative is
[C′(x)=−dfrac{3000}{r^2}+2r.]
Therefore, (C′(r)=0) when (2r=dfrac{3000}{r^2}). Solving this equation for (r), we obtain (r^3=1500), so (r=sqrt[3]{1500}.) Since this is the only critical point of (C), the absolute minimum must occur at (r=sqrt[3]{1500}).
When (r=sqrt[3]{1500}), (h= dfrac{300}{pi {sqrt[3]{1500}}^2}). Therefore, the dimensions of the can sho uld be (r=sqrt[3]{1500}in.) and ( h= dfrac{300}{pi {sqrt[3]{1500}}^2}).
With these dimensions, the cost is
Exercise (PageIndex{9})
Pop cans to hold (300) ml are made in the shape of right circular cylinders. Find the dimensions of the can that minimize the surface area.
Add answer text here and it will automatically be hidden if you have a 'AutoNum' template active on the page.
Example (PageIndex{10}): Closest point
Find the point on the curve (y=frac{-x^2}{3}) that is closest to the point (P(4,-1).)
In the exercises, you will see a variety of situations that require you to combine problem--solving skills with calculus. Focus on the process; learn how to form equations from situations that can be manipulated into what you need. Eschew memorizing how to do 'this kind of problem' as opposed to 'that kind of problem.' Learning a process will benefit one far longer than memorizing a specific technique.
5.6 Optimization Problemsap Calculus Solver
The next section introduces our final application of the derivative: differentials. Given (y=f(x)), they offer a method of approximating the change in (y) after (x) changes by a small amount.
Key Concepts
- To solve an optimization problem, begin by drawing a picture and introducing variables.
- Find an equation relating the variables.
- Find a function of one variable to describe the quantity that is to be minimized or maximized.
- Look for critical points to locate local extrema.
Glossary
- optimization problems
- problems that are solved by finding the maximum or minimum value of a function
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Gregory Hartman (Virginia Military Institute). Contributions were made by Troy Siemers and Dimplekumar Chalishajar of VMI and Brian Heinold of Mount Saint Mary's University. This content is copyrighted by a Creative Commons Attribution - Noncommercial (BY-NC) License. http://www.apexcalculus.com/
Integrated by Justin Marshall.
Pamini Thangarajah (Mount Royal University, Calgary, Alberta, Canada)
Here are a set of practice problems for the Calculus I notes. Click on the 'Solution' link for each problem to go to the page containing the solution.
Note that some sections will have more problems than others and some will have more or less of a variety of problems. Most sections should have a range of difficulty levels in the problems although this will vary from section to section.
Here is a listing of sections for which practice problems have been written as well as a brief description of the material covered in the notes for that particular section.
Review - In this chapter we give a brief review of selected topics from Algebra and Trig that are vital to surviving a Calculus course. Included are Functions, Trig Functions, Solving Trig Equations and Equations, Exponential/Logarithm Functions and Solving Exponential/Logarithm Equations.Inverse Functions – In this section we will define an inverse function and the notation used for inverse functions. We will also discuss the process for finding an inverse function.
Trig Functions – In this section we will give a quick review of trig functions. We will cover the basic notation, relationship between the trig functions, the right triangle definition of the trig functions. We will also cover evaluation of trig functions as well as the unit circle (one of the most important ideas from a trig class!) and how it can be used to evaluate trig functions.
Solving Trig Equations – In this section we will discuss how to solve trig equations. The answers to the equations in this section will all be one of the “standard” angles that most students have memorized after a trig class. However, the process used here can be used for any answer regardless of it being one of the standard angles or not.
Solving Trig Equations with Calculators, Part I – In this section we will discuss solving trig equations when the answer will (generally) require the use of a calculator (i.e. they aren’t one of the standard angles). Note however, the process used here is identical to that for when the answer is one of the standard angles. The only difference is that the answers in here can be a little messy due to the need of a calculator. Included is a brief discussion of inverse trig functions.
Solving Trig Equations with Calculators, Part II – In this section we will continue our discussion of solving trig equations when a calculator is needed to get the answer. The equations in this section tend to be a little trickier than the 'normal' trig equation and are not always covered in a trig class.
Exponential Functions –In this section we will discuss exponential functions. We will cover the basic definition of an exponential function, the natural exponential function, i.e. ({bf e}^{x}), as well as the properties and graphs of exponential functions
Logarithm Functions – In this section we will discuss logarithm functions, evaluation of logarithms and their properties. We will discuss many of the basic manipulations of logarithms that commonly occur in Calculus (and higher) classes. Included is a discussion of the natural ((ln(x))) and common logarithm ((log(x))) as well as the change of base formula.
Exponential and Logarithm Equations – In this section we will discuss various methods for solving equations that involve exponential functions or logarithm functions.
Common Graphs – In this section we will do a very quick review of many of the most common functions and their graphs that typically show up in a Calculus class.
Limits - In this chapter we introduce the concept of limits. We will discuss the interpretation/meaning of a limit, how to evaluate limits, the definition and evaluation of one-sided limits, evaluation of infinite limits, evaluation of limits at infinity, continuity and the Intermediate Value Theorem. We will also give a brief introduction to a precise definition of the limit and how to use it to evaluate limits
The Limit – In this section we will introduce the notation of the limit. We will also take a conceptual look at limits and try to get a grasp on just what they are and what they can tell us. We will be estimating the value of limits in this section to help us understand what they tell us. We will actually start computing limits in a couple of sections.
One-Sided Limits – In this section we will introduce the concept of one-sided limits. We will discuss the differences between one-sided limits and limits as well as how they are related to each other.
Limit Properties – In this section we will discuss the properties of limits that we’ll need to use in computing limits (as opposed to estimating them as we've done to this point). We will also compute a couple of basic limits in this section.
Computing Limits – In this section we will looks at several types of limits that require some work before we can use the limit properties to compute them. We will also look at computing limits of piecewise functions and use of the Squeeze Theorem to compute some limits.
Infinite Limits – In this section we will look at limits that have a value of infinity or negative infinity. We’ll also take a brief look at vertical asymptotes.
Limits At Infinity, Part I – In this section we will start looking at limits at infinity, i.e. limits in which the variable gets very large in either the positive or negative sense. We will concentrate on polynomials and rational expressions in this section. We’ll also take a brief look at horizontal asymptotes.
Limits At Infinity, Part II – In this section we will continue covering limits at infinity. We’ll be looking at exponentials, logarithms and inverse tangents in this section.
Continuity – In this section we will introduce the concept of continuity and how it relates to limits. We will also see the Intermediate Value Theorem in this section and how it can be used to determine if functions have solutions in a given interval.
The Definition of the Limit – In this section we will give a precise definition of several of the limits covered in this section. We will work several basic examples illustrating how to use this precise definition to compute a limit. We’ll also give a precise definition of continuity..
Derivatives - In this chapter we introduce Derivatives. We cover the standard derivatives formulas including the product rule, quotient rule and chain rule as well as derivatives of polynomials, roots, trig functions, inverse trig functions, hyperbolic functions, exponential functions and logarithm functions. We also cover implicit differentiation, related rates, higher order derivatives and logarithmic differentiation.
Interpretation of the Derivative – In this section we give several of the more important interpretations of the derivative. We discuss the rate of change of a function, the velocity of a moving object and the slope of the tangent line to a graph of a function.
Differentiation Formulas – In this section we give most of the general derivative formulas and properties used when taking the derivative of a function. Examples in this section concentrate mostly on polynomials, roots and more generally variables raised to powers.
Product and Quotient Rule – In this section we will give two of the more important formulas for differentiating functions. We will discuss the Product Rule and the Quotient Rule allowing us to differentiate functions that, up to this point, we were unable to differentiate.
Derivatives of Trig Functions – In this section we will discuss differentiating trig functions. Derivatives of all six trig functions are given and we show the derivation of the derivative of (sin(x)) and (tan(x)).
Derivatives of Exponential and Logarithm Functions – In this section we derive the formulas for the derivatives of the exponential and logarithm functions.
Derivatives of Inverse Trig Functions – In this section we give the derivatives of all six inverse trig functions. We show the derivation of the formulas for inverse sine, inverse cosine and inverse tangent.
Derivatives of Hyperbolic Functions – In this section we define the hyperbolic functions, give the relationships between them and some of the basic facts involving hyperbolic functions. We also give the derivatives of each of the six hyperbolic functions and show the derivation of the formula for hyperbolic sine.
Chain Rule – In this section we discuss one of the more useful and important differentiation formulas, The Chain Rule. With the chain rule in hand we will be able to differentiate a much wider variety of functions. As you will see throughout the rest of your Calculus courses a great many of derivatives you take will involve the chain rule!
Implicit Differentiation – In this section we will discuss implicit differentiation. Not every function can be explicitly written in terms of the independent variable, e.g. y = f(x) and yet we will still need to know what f'(x) is. Implicit differentiation will allow us to find the derivative in these cases. Knowing implicit differentiation will allow us to do one of the more important applications of derivatives, Related Rates (the next section).
Related Rates – In this section we will discuss the only application of derivatives in this section, Related Rates. In related rates problems we are give the rate of change of one quantity in a problem and asked to determine the rate of one (or more) quantities in the problem. This is often one of the more difficult sections for students. We work quite a few problems in this section so hopefully by the end of this section you will get a decent understanding on how these problems work.
Higher Order Derivatives – In this section we define the concept of higher order derivatives and give a quick application of the second order derivative and show how implicit differentiation works for higher order derivatives.
Logarithmic Differentiation – In this section we will discuss logarithmic differentiation. Logarithmic differentiation gives an alternative method for differentiating products and quotients (sometimes easier than using product and quotient rule). More importantly, however, is the fact that logarithm differentiation allows us to differentiate functions that are in the form of one function raised to another function, i.e. there are variables in both the base and exponent of the function.
Applications of Derivatives - In this chapter we will cover many of the major applications of derivatives. Applications included are determining absolute and relative minimum and maximum function values (both with and without constraints), sketching the graph of a function without using a computational aid, determining the Linear Approximation of a function, L’Hospital’s Rule (allowing us to compute some limits we could not prior to this), Newton's Method (allowing us to approximate solutions to equations) as well as a few basic Business applications.
Critical Points – In this section we give the definition of critical points. Critical points will show up in most of the sections in this chapter, so it will be important to understand them and how to find them. We will work a number of examples illustrating how to find them for a wide variety of functions.
Minimum and Maximum Values – In this section we define absolute (or global) minimum and maximum values of a function and relative (or local) minimum and maximum values of a function. It is important to understand the difference between the two types of minimum/maximum (collectively called extrema) values for many of the applications in this chapter and so we use a variety of examples to help with this. We also give the Extreme Value Theorem and Fermat's Theorem, both of which are very important in the many of the applications we'll see in this chapter.
Finding Absolute Extrema – In this section we discuss how to find the absolute (or global) minimum and maximum values of a function. In other words, we will be finding the largest and smallest values that a function will have.
The Shape of a Graph, Part I – In this section we will discuss what the first derivative of a function can tell us about the graph of a function. The first derivative will allow us to identify the relative (or local) minimum and maximum values of a function and where a function will be increasing and decreasing. We will also give the First Derivative test which will allow us to classify critical points as relative minimums, relative maximums or neither a minimum or a maximum.
The Shape of a Graph, Part II – In this section we will discuss what the second derivative of a function can tell us about the graph of a function. The second derivative will allow us to determine where the graph of a function is concave up and concave down. The second derivative will also allow us to identify any inflection points (i.e. where concavity changes) that a function may have. We will also give the Second Derivative Test that will give an alternative method for identifying some critical points (but not all) as relative minimums or relative maximums.
The Mean Value Theorem – In this section we will give Rolle's Theorem and the Mean Value Theorem. With the Mean Value Theorem we will prove a couple of very nice facts, one of which will be very useful in the next chapter.
Optimization Problems – In this section we will be determining the absolute minimum and/or maximum of a function that depends on two variables given some constraint, or relationship, that the two variables must always satisfy. We will discuss several methods for determining the absolute minimum or maximum of the function. Examples in this section tend to center around geometric objects such as squares, boxes, cylinders, etc.
More Optimization Problems – In this section we will continue working optimization problems. The examples in this section tend to be a little more involved and will often involve situations that will be more easily described with a sketch as opposed to the 'simple' geometric objects we looked at in the previous section.
L’Hospital’s Rule and Indeterminate Forms – In this section we will revisit indeterminate forms and limits and take a look at L’Hospital’s Rule. L’Hospital’s Rule will allow us to evaluate some limits we were not able to previously.
Linear Approximations – In this section we discuss using the derivative to compute a linear approximation to a function. We can use the lienar approximation to a function to approximate values of the function at certain points. While it might not seem like a useful thing to do with when we have the function there really are reasons that one might want to do this. We give two ways this can be useful in the examples.
Differentials – In this section we will compute the differential for a function. We will give an application of differentials in this section. However, one of the more important uses of differentials will come in the next chapter and unfortunately we will not be able to discuss it until then.
Newton’s Method – In this section we will discuss Newton's Method. Newton's Method is an application of derivatives will allow us to approximate solutions to an equation. There are many equations that cannot be solved directly and with this method we can get approximations to the solutions to many of those equations.
Business Applications – In this section we will give a cursory discussion of some basic applications of derivatives to the business field. We will revisit finding the maximum and/or minimum function value and we will define the marginal cost function, the average cost, the revenue function, the marginal revenue function and the marginal profit function. Note that this section is only intended to introduce these concepts and not teach you everything about them.
Integrals - In this chapter we will give an introduction to definite and indefinite integrals. We will discuss the definition and properties of each type of integral as well as how to compute them including the Substitution Rule. We will give the Fundamental Theorem of Calculus showing the relationship between derivatives and integrals. We will also discuss the Area Problem, an important interpretation of the definite integral.
Computing Indefinite Integrals – In this section we will compute some indefinite integrals. The integrals in this section will tend to be those that do not require a lot of manipulation of the function we are integrating in order to actually compute the integral. As we will see starting in the next section many integrals do require some manipulation of the function before we can actually do the integral. We will also take a quick look at an application of indefinite integrals.
Substitution Rule for Indefinite Integrals – In this section we will start using one of the more common and useful integration techniques – The Substitution Rule. With the substitution rule we will be able integrate a wider variety of functions. The integrals in this section will all require some manipulation of the function prior to integrating unlike most of the integrals from the previous section where all we really needed were the basic integration formulas.
More Substitution Rule – In this section we will continue to look at the substitution rule. The problems in this section will tend to be a little more involved than those in the previous section.
Area Problem – In this section we start off with the motivation for definite integrals and give one of the interpretations of definite integrals. We will be approximating the amount of area that lies between a function and the (x)-axis. As we will see in the next section this problem will lead us to the definition of the definite integral and will be one of the main interpretations of the definite integral that we'll be looking at in this material.
Definition of the Definite Integral – In this section we will formally define the definite integral, give many of its properties and discuss a couple of interpretations of the definite integral. We will also look at the first part of the Fundamental Theorem of Calculus which shows the very close relationship between derivatives and integrals
Computing Definite Integrals – In this section we will take a look at the second part of the Fundamental Theorem of Calculus. This will show us how we compute definite integrals without using (the often very unpleasant) definition. The examples in this section can all be done with a basic knowledge of indefinite integrals and will not require the use of the substitution rule. Included in the examples in this section are computing definite integrals of piecewise and absolute value functions.
Substitution Rule for Definite Integrals – In this section we will revisit the substitution rule as it applies to definite integrals. The only real requirements to being able to do the examples in this section are being able to do the substitution rule for indefinite integrals and understanding how to compute definite integrals in general.
Applications of Integrals - In this chapter we will take a look at some applications of integrals. We will look at Average Function Value, Area Between Curves, Volume (both solids of revolution and other solids) and Work.
Area Between Curves – In this section we’ll take a look at one of the main applications of definite integrals in this chapter. We will determine the area of the region bounded by two curves.
Volumes of Solids of Revolution / Method of Rings – In this section, the first of two sections devoted to finding the volume of a solid of revolution, we will look at the method of rings/disks to find the volume of the object we get by rotating a region bounded by two curves (one of which may be the (x) or (y)-axis) around a vertical or horizontal axis of rotation.
Volumes of Solids of Revolution / Method of Cylinders – In this section, the second of two sections devoted to finding the volume of a solid of revolution, we will look at the method of cylinders/shells to find the volume of the object we get by rotating a region bounded by two curves (one of which may be the (x) or (y)-axis) around a vertical or horizontal axis of rotation.
More Volume Problems – In the previous two sections we looked at solids that could be found by treating them as a solid of revolution. Not all solids can be thought of as solids of revolution and, in fact, not all solids of revolution can be easily dealt with using the methods from the previous two sections. So, in this section we’ll take a look at finding the volume of some solids that are either not solids of revolutions or are not easy to do as a solid of revolution.
Work – In this section we will look at is determining the amount of work required to move an object subject to a force over a given distance.

Comments are closed.